Errors or Misconception
Before we start thinking about misconceptions* in the teaching and learning of fractions let us think about the difference between an error and a misconception
an error is an inaccuracy, but a misconception is the result of misunderstanding
Errors occur because of lapses in concentration or hasty reasoning or a failure to notice important features of a problem, whereas a misconception is a mistake in conceptual understanding (for example a very common misconception is that division makes the number smaller, or when you multiply two numbers the answer is always gets bigger). However, misconceptions should not be dismissed as ‘wrong thinking’; they may well be an absolute necessity in the learners’ conceptual development process.
Fraction Misconceptions
Learners not understanding the role of the denominator as the total number of equal parts that make up a whole (unity).
Learners not understanding why a 
is bigger than a 
Learners not understanding the language of fractions, for example 
is the same as 
.
More precisely we might the equivalence of language. Taking this a step further 
teachers often just state a rule 
without exploring the language.
“How many ‘s are there in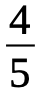 
”
Learners not understanding that is the same as 4 ÷ 5 and 0.8. ( I find the notation 4/5 really unhelpful and should be avoided).
Learners not understanding that
is not the same as 5%.
